TA8: Maksimum Deflection of a Simply Supported Beam
1.PROBLEM DESCRIPTION
A simply supported beam is subjected to a distributed load, p. The beam is made of wood and modulus of elasticity is known. Height, width and length of the beam is also given. We are asked to find the maximum deflection of the beam.
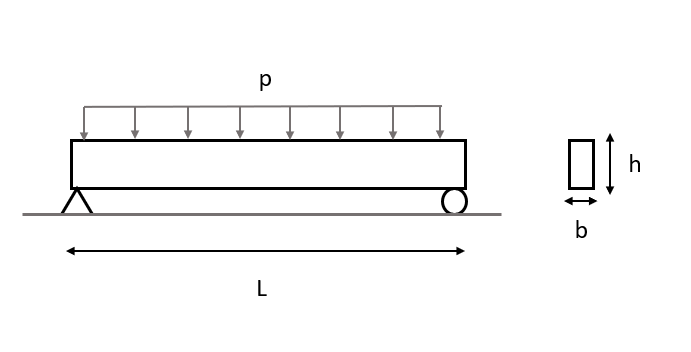
Material Properties |
Geometric Properties |
Loading |
|---|---|---|
E = 10 GPa |
L = 3 m, b = 0.06 m, h = 0.125 m |
p = 2000 N/m |
2.MODEL SETUP AND SOLUTION
The following sections describe the setup and solution steps for this tutorial:
2.1. Preparation
1.First we will import our libraries, that we will use almost in each tutorial, from Simularge Libraries to our empty Python page .
1from TwinAPI.SimulationTools import Solver
2from TwinAPI.SimulationTools import Mesher
Material properties are significant factors that affect the result. Therefore, we should be able to define them easily. Below I will explain how to use and write Material Library elaborately. Furthermore, the libraries which has to be imported for this problem is given below.
1from TwinAPI.MaterialLibrary import MaterialManager
2from TwinAPI.MaterialLibrary.Units import units
2.2. General Settings
After the necessary libraries are imported into the analysis, the analysis is defined.
1.Define the name of the analysis as “SimSupBeam”
1SimSupBeam= Solver.Analysis(Verbose=True)
2.Calculix is used for solid mechanics problems in TwinAPI. Hence, we define Calculix as the solver for this analysis.
1SimSupBeam.SetSolver("Calculix")
Analysis is defined successfully into TwinAPI system.
2.3. Geometry/Mesh
There are two different options to define the geometry on TwinAPI system. You can create the geometry on TwinAPI by using Mesher Library which is one of Simularge libraries or you can import your own CAD geometry.
1 b=0.06
2 h=0.125
3 L=3
4 NodeX=200
5 NodeY=10
6 NodeZ=10
7 directionX=">"
8 directionY="<>"
9 directionZ="<>"
10 TypeX="uniform"
11 TypeY="uniform"
12 TypeZ="uniform"
13 TransX=0
14 TransY=0
15 TransZ=0
16
17 box=Mesher.box(L,NodeX,TypeX,directionX,h,NodeY,TypeY,directionY, b,NodeZ,TypeZ,directionZ, TransX,TransY,TransZ)
With the script given above, you can create your geometry and mesh.
L= Length in the x-direction
NodeX= Node Number in the x-direction
directionX= Aspect
TypeX= Mesh type inthe x-direction.
TransX= Translation in the x-irection
All of given above is valid for y- and z-direction.
We create a box geometry with the name “box” from given inputs.
Note
We told you that you can also create this geometry by importing 3D CAD file apart from using MESHER. Code should be written like this;
1 Box1=Mesher.MeshFromCad('Box.step',20000,1,1e4,SurfaceExtract=True)
If we are not sure how the created geometry is and want to see the geometry before starting analysis;
Click Preview Button

2.4. Material
Before we start, there are lots of parameters which will affect the result of the problem. We are going to explain which parameters are required for this problem and some parameter instances will be given.
We call the Material class in the Material Manager library and name the material as “TwinAPI”. At the same time, we give the information that the material behaves as wood by typing “wood”.
Our material will behave elastically, therefore we type “Elastic”. Only modulus of elasticity is required for this problem.
1 material = MaterialManager.Material("TwinAPI","wood")
2
3 material.SetMechanicType("Elastic")
4 material.SetMechanicData("youngsModulus",1e10 ,units["pa"])
Other examples of parameters in Material Library are given below.
1 material.SetGeneralData("density", 7860, units["kg/m3"])
2
3 material.SetMechanicData("poissonsRatio", 0.39)
After defining the material into our system, we should combine geometry defined above and material using AddPart.
1SimSupBeam.AddPart(box,material)
2
3SimSupBeam.Assemble()
2.5. Boundary Conditions
After adding material and geometry to the analysis, we are ready to set the boundary conditions.
1.First of all, we will create a step with the name “Step1”.
1Step1=Solver.CreateStep("new")
2.We need to choose whether this step is computed depending on time or not. Since our problem is steady-state, the code below should be used.
1Step1.Time("SteadyState",[0,0.5,0.1])
If the problem was transient, type of the problem and time for the analysis would be written in a similar manner to the code given below.
1Step1.Time("Transient",[0,10,0.1])
3.Since a simply supported beam has a pin support at one end and a roller support at the other end, we define the boundary conditions as given below. We define the load as “Pressure” and the distributed load is divided by the width of the beam to calculate the pressure.
1Step1.AddBC("Fix",[box.right],[("X",0)],"")
2Step1.AddBC("Fix",[box.right],[("Y",0)],"")
3Step1.AddBC("Fix",[box.right],[("Z",0)],"")
4
5Step1.AddBC("Fix",[box.left],[("Y",0)],"")
6
7Step1.AddBC("Pressure",[box.top],[("Y",-2000/0.06)],"N/m2")
2.6. Solution
After defining our boundary conditions, we need to combine our defined domain and the steps containing boundary conditions.To complete this task;
1SimSupBeam.Build([Step1])
Now,the problem is ready to be solved.
1SimSupBeam.Solve()
Let’s review what we have done.

2.7. Processing
Click Run Button and gears will rotate on the right side while problem is being solved.
2.8. Post-Processing
2.After problem solved;
We can see the result;
Click Result Button
3.If we want to see the detailed result of the problem;
Output tab shows us the results that we desire to see.
1Disp=SimSupBeam.Result(Variable="Displacement Y", Set=box.top)
2print("Maximum Deflection:" ,max(Disp))
Log tab tells us respectively what happened in the analysis.
Error tab shows us if there is an error in the script, it tells us what the error is and where it is.
Files tab includes the files imported using Upload button.
Graph tab shows us analysis result viewed graphically. (It will be shown in other examples.)
3.SUMMARY
In this tutorial, we learned how to set up and solve a problem involving a simply supported beam. We also learned how to perform postprocessing in an engineering manner.
The table given below shows comparison of the result of theoritical solution and the result obtained from TwinAPI.
SOLID MODEL |
Target |
SIMULARGE-TwinAPI |
Ratio: SIMULARGE/Target |
|---|---|---|---|
Maximum Deflection, mm |
21.6 mm |
22.0 mm |
1.02 |
4. SOURCE CODE
1from TwinAPI.MaterialLibrary import MaterialManager
2from TwinAPI.MaterialLibrary.Units import units
3from TwinAPI.SimulationTools import Solver
4from TwinAPI.SimulationTools import Mesher
5
6SimSupBeam= Solver.Analysis(Verbose=True)
7SimSupBeam.SetSolver("Calculix")
8
9b=0.06
10h=0.125
11L=3
12NodeX=150
13NodeY=10
14NodeZ=10
15directionX=">"
16directionY="<>"
17directionZ=directionY
18TypeX="uniform"
19TypeY=TypeX
20TypeZ=TypeX
21TransX=0
22TransY=0
23TransZ=0
24
25box=Mesher.box(L,NodeX,TypeX,directionX,h,NodeY,TypeY,directionY, b,NodeZ,TypeZ,directionZ, TransX,TransY,TransZ)
26
27material = MaterialManager.Material("TwinAPI","wood")
28
29material.SetMechanicType("Elastic")
30material.SetMechanicData("youngsModulus",1e10,units["pa"])
31
32SimSupBeam.AddPart(box,material)
33
34SimSupBeam.Assemble()
35Step1=Solver.CreateStep("new")
36Step1.Time("SteadyState",[0,0.5,0.1])
37
38Step1.AddBC("Fix",[box.right],[("X",0)],"")
39Step1.AddBC("Fix",[box.right],[("Y",0)],"")
40Step1.AddBC("Fix",[box.right],[("Z",0)],"")
41
42Step1.AddBC("Fix",[box.left],[("Y",0)],"")
43
44Step1.AddBC("Pressure",[box.top],[("Y",-2000/0.06)],"N/m2")
45
46SimSupBeam.Build([Step1])
47SimSupBeam.Solve()
48
49Disp=SimSupBeam.Result(Variable="Displacement Y", Set=box.top)
50print("Maximum Deflection:" ,max(Disp))
Keywords: Maximum Deflection, Simply Supported Beam, Distributed Load
Problem Reference: R. C. Hibbeler, Mechanics Of Materials, 10th Edition in SI Units, Pearson Education, Inc., London, England, 2018, pg. 611, F12-4.
Author: Ilknur Akica