TA6: Self Weight of a Cantilever Beam (Under Revision)
1.PROBLEM DESCRIPTION
The aim of this tutorial is observing the deflection caused by the weight of the beam itself. The beam with a rectangular cross-section is fixed to the Wall. The cross-sectional area and length of the beam are given. The beam is to be made of steel with a modulus of elasticity of 200 GPa. Density of the steel is 7.86 kg/m3 and Poissons’s ratio is 0.3 .
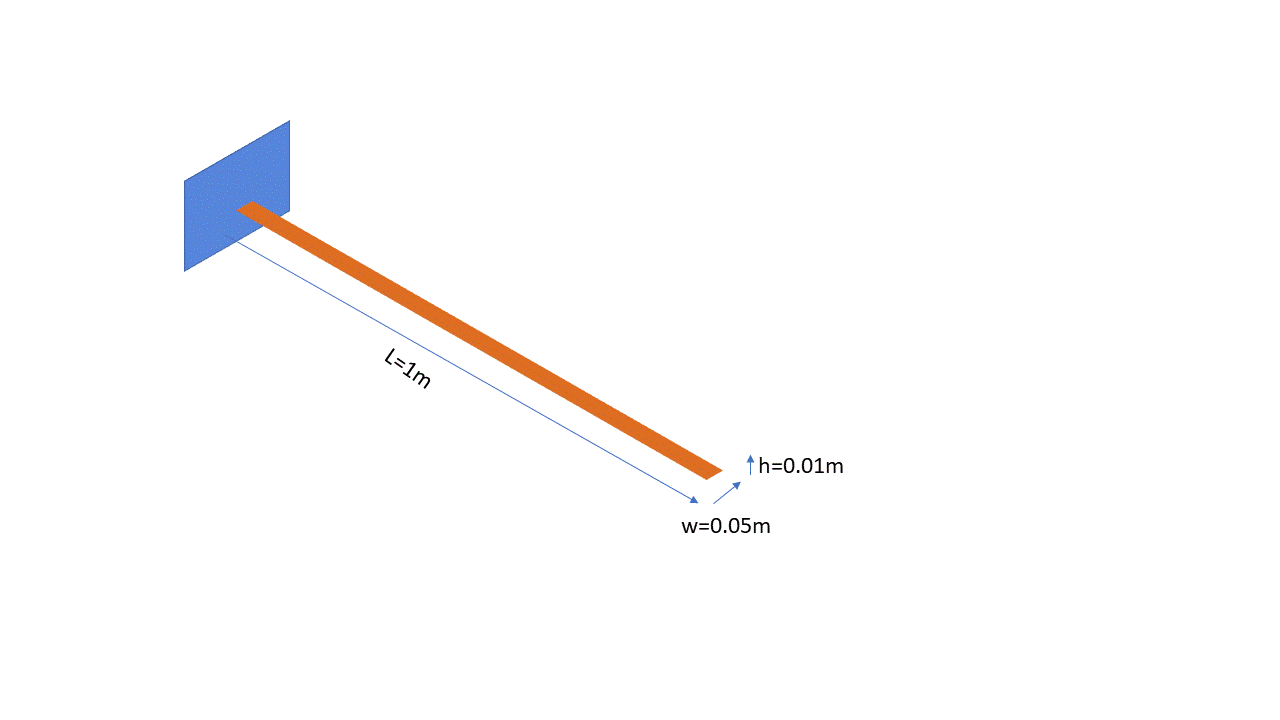
Material Properties |
Geometric Properties |
|---|---|
Young’s Modulus = 200 GPa |
L = 1 m |
Poisson’s Ratio = 0.3 |
h = 0.01 m |
Density = 7.86 kg/m3 |
w = 0.05 m |
2.MODEL SETUP AND SOLUTION
The following sections describe the setup and solution steps for this tutorial:
2.1. Preparation
To run this tutorial;
1.You must sign up and log in. —->>>>> TwinAPI
2.After login, Click Personel Projects>>New Project button on the screen and then we will create a project page by giving the project name.
(Let’s name of Analysis “SelfWeightofCantileverBeam”)
3.You can see the project page on your Personel Project Part.
4.Our Screen is a blank python page without any script. We will be doing a tutorial by using Simularge’s Library.
5.We import our libraries from the Simularge Libraries to our empty Python page that we almost will use in each tutorial.
1from TwinAPI.SimulationTools import Solver
2from TwinAPI.SimulationTools import Mesher
Material Properties is one of the most significant factor that affect to result. Therefore,we should define it easily to the problem. I will explain below how to use and write Material Library elaborately. Furtherless, The Libraries that has to imported to problem is given below.
1from TwinAPI.MaterialLibrary import MaterialManager
2from TwinAPI.MaterialLibrary.Units import units
2.2. General Settings
After the necessary libraries are imported into the analysis, analysis are defined.
1.Defined name of Analysis as “SelfWeightofCantileverBeam”
1SelfWeightofCantileverBeam= Solver.Analysis(Verbose=True)
2.Calculix is used on solid mechanics problems in TwinAPI. Hence, we are defining Calculix to run this analysis.
1SelfWeightofCantileverBeam.SetSolver("Calculix")
Analysis is defined successfully into TwinAPI System.

2.3. Geometry/Mesh
There is two different options to define geometry on TwinAPI System. Create own geometry on TwinAPI by using Mesher Library that belong to Simularge’s libraries or You can import own CAD Geometry.
1LengthX=1 #m
2LengthY=0.01 #m
3LengthZ=0.05 #m
4NodeX=800
5NodeY=5
6NodeZ=10
7Trans_X=0
8Trans_Y=0
9Trans_Z=0
10directionX=''
11directionY=''
12directionZ=''
13typeX='uniform'
14typeY='uniform'
15typeZ='uniform'
16box1=Mesher.box(LengthX,NodeX,typeX,directionX,LengthY,NodeY,typeY,directionY, LengthZ,NodeZ,typeZ,directionZ, Trans_X,Trans_Y,Trans_Z)
With the script given above, you can create your box geometry and mesh.
LengthX= Length of X Direction
NodeX= Node Number of X Direction
Trans_X= Translation of X Direction
directionX= Aspect
typeX= Mesh type of X direction.
All of given above is valid for Y and Z Direction.
We create a box geometry that name is “box1” from given inputs.
Note
We told you that you can also create this geometry import 3D CAD file apart from using MESHER. Code should be written like this;
1 Box1=Mesher.MeshFromCad('Box.step',20000,1,1e4,SurfaceExtract=True)
If we are not sure how created geometry and want to see geometry before starting analysis;
Click Preview Button

2.4. Material
Before we started,There are lots of parameters to impact to result of problem. We are going to explain which parameters are requirement for problem first. Later, We would give an parameters instances which can be used.
If your material is isotropic thats means all properties is equal with different direction. However Anisotropic Material Properties is not the same value with different direction. Modulus of Elasticity and density of material will impact amount of deflection in this problem.
We call the Material class in the Material Manager library and name the material “Material_name”. At the same time, We give the information that the material behaves as a steel by typing “steel”.
1 material = MaterialManager.Material("Material_name","steel")
2
3 material.SetGeneralData("density",7.86,units["kg/m3"])
4
5 material.SetMechanicType("Elastic")
6 material.SetMechanicData("youngsModulus",200e9,units["pa"])
7 material.SetMechanicData("poissonsRatio",0.3)
We will make an example to understand better what can be used parameters in Material Library.
1 material.SetThermalData("specificHeat",7,units["j/kgk"])
2
3 material.SetThermalData("expansionCoefficient",10,units["1/k"])
4
5 material.SetThermalData("conductivity",25,units["btu/hr*ft*F"])
After defining the material into our system, we should combine geometry define above and material using Addpart method.
1SelfWeightofCantileverBeam.AddPart(box1,material)
2
3SelfWeightofCantileverBeam.Assemble()
2.5. Boundary Conditions
After adding material and geometry to the analysis, we are ready to set the boundary conditions.
1.First of all, we need to call a method to create a step. Step1’s name can be change.
1Step1=Solver.CreateStep("new")
2.We need to choose whether this step is computed depending on time or not.Explained problem is Steady-State. Therefore,below code should be written.
1Step1.Time("SteadyState")
If the Problem was Transient,type of problem and time of analysis should be written in a similar manner with below code.
1Step1.Time("Transient",[0.1,10,0.1])
3.The type of boundary condition is fixed for this problem. Also we should define gravity in order to observe its effect.
1Step1.AddBC("Fix",[box1.left],[("X",0)],"")
2Step1.AddBC("Fix",[box1.left],[("Y",0)],"")
3Step1.AddBC("Fix",[box1.left],[("Z",0)],"")
4
5Step1.AddBC("gravity",[box1.All],[("Y",-9.81)],"m/s2")
2.6. Solution
After defining our boundary conditions, we need to combine our defined domain and the steps containing boundary conditions.To complete this task;
1SelfWeightofCantileverBeam.Build([Step1])
Now,Problem is ready to be solved.
1SelfWeightofCantileverBeam.Solve()
Before going to be PostProcess Stage, we can review what we have done.

2.7. Processing
Click Run Button and gears rotate on right side while problem is being solved.
2.8. Post-Processing
2.After Problem solved;
We can see result;
Click Result Button
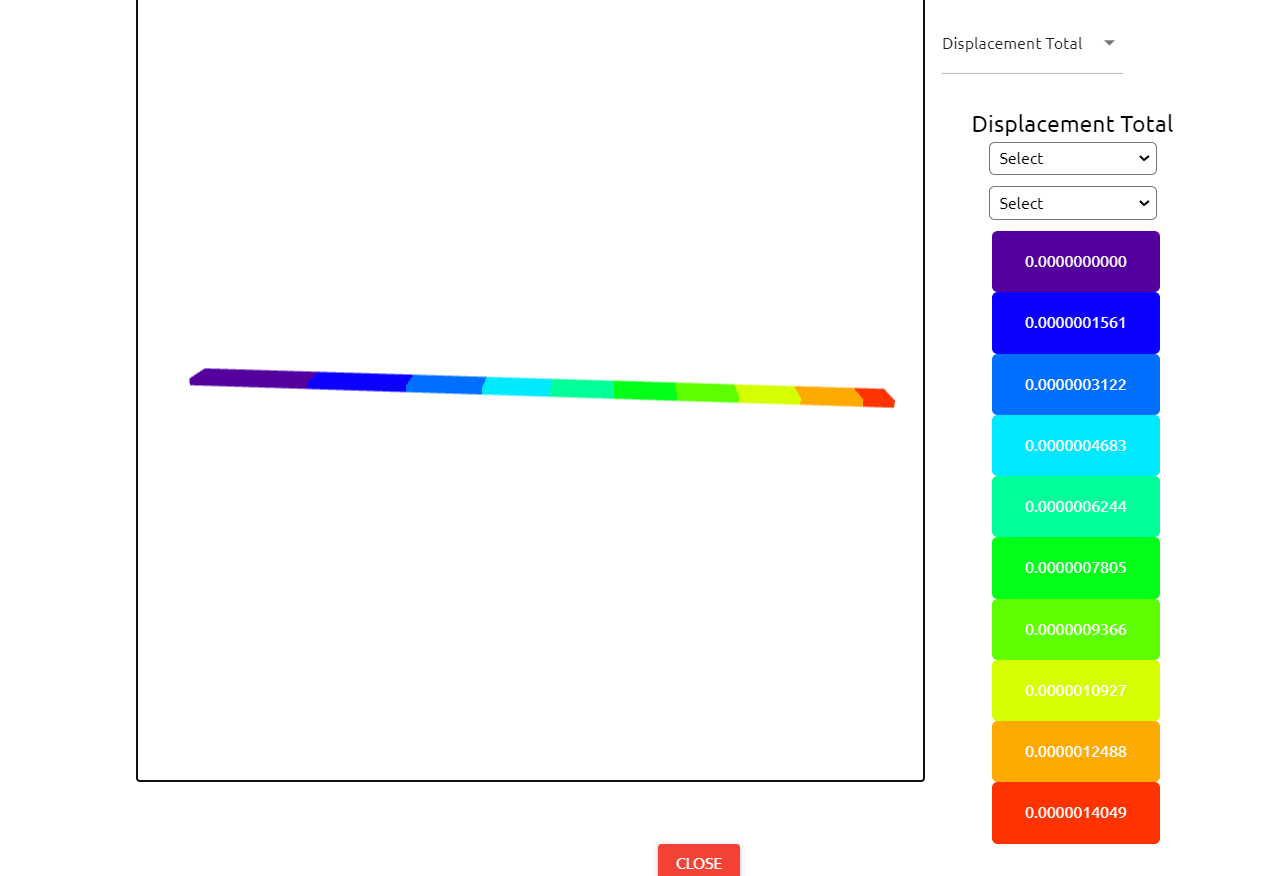
3.If we want to see detailed result about problem;
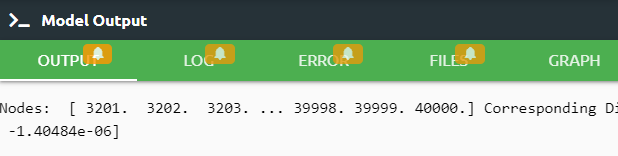
Output Tab shows us the results that we desire to see. By using print line we could see the result in the Output section.
1t2=SelfWeightofCantileverBeam.Result(Variable="Displacement Y", Set=box1.top)
2print("Nodes: ",box1.top[0],"Corresponding Disp: ", t2)
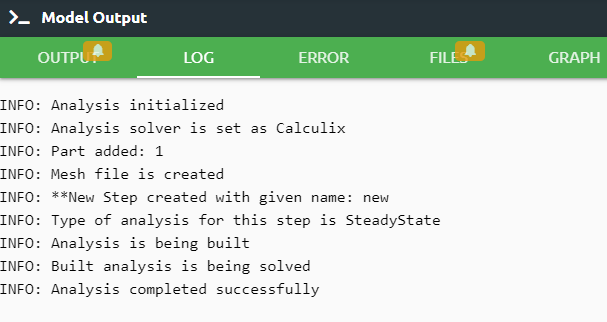
Log tab tells us respectively what happened in analysis.
Error tab shows us if there is an error in script, It tells us what the error is and where it is.
Files tab can upload the files to be imported from the Upload command and check them from Files.
Graph tab shows us analysis result can be viewed graphically. (It will be shown in other examples.)
3.SUMMARY
In this tutorial, we learned how to observe the deflection caused by the weight of the beam itself on TwinAPI. We also learned how to perform postprocessing in an engineering manner.
With table given below shows that comparasion of Ansys Mechanical Result and TwinAPI result.
MODEL |
Target |
ANSYS |
SIMULARGE-TwinAPI |
Error:ANSYS |
Error:TwinAPI |
|---|---|---|---|---|---|
Max Deflection |
5.777e-6 |
5.777e-6 |
5.619e-6 |
%0 |
%2.735 |
4. SOURCE CODE
1from TwinAPI.SimulationTools import Solver
2from TwinAPI.SimulationTools import Mesher
3from TwinAPI.MaterialLibrary import MaterialManager
4from TwinAPI.MaterialLibrary.Units import units
5
6SelfWeightofCantileverBeam= Solver.Analysis(Verbose=True)
7SelfWeightofCantileverBeam.SetSolver("Calculix")
8
9LengthX=1 #m
10LengthY=0.01 #m
11LengthZ=0.05 #m
12NodeX=800
13NodeY=5
14NodeZ=10
15Trans_X=0
16Trans_Y=0
17Trans_Z=0
18directionX=''
19directionY=''
20directionZ=''
21typeX='uniform'
22typeY='uniform'
23typeZ='uniform'
24box1=Mesher.box(LengthX,NodeX,typeX,directionX,LengthY,NodeY,typeY,directionY, LengthZ,NodeZ,typeZ,directionZ, Trans_X,Trans_Y,Trans_Z)
25
26material = MaterialManager.Material("Material_name","steel")
27material.SetGeneralData("density",7.86,units["kg/m3"])
28
29material.SetMechanicType("Elastic")
30material.SetMechanicData("youngsModulus",200e9,units["pa"])
31material.SetMechanicData("poissonsRatio",0.3)
32
33SelfWeightofCantileverBeam.AddPart(box1,material)
34
35SelfWeightofCantileverBeam.Assemble()
36
37Step1=Solver.CreateStep("new")
38Step1.Time("SteadyState")
39
40Step1.AddBC("Fix",[box1.left],[("X",0)],"")
41Step1.AddBC("Fix",[box1.left],[("Y",0)],"")
42Step1.AddBC("Fix",[box1.left],[("Z",0)],"")
43
44Step1.AddBC("gravity",[box1.All],[("Y",-9.81)],"m/s2")
45
46SelfWeightofCantileverBeam.Build([Step1])
47SelfWeightofCantileverBeam.Solve()
48
49t2=SelfWeightofCantileverBeam.Result(Variable="Displacement Y", Set=box1.top)
50print("Nodes: ",box1.top[0],"Corresponding Disp: ", t2)
Keywords: Self Weight, Deflection, Gravity, Displacement
Problem Reference: UofA ANSYS Tutorial, https://sites.ualberta.ca/~wmoussa/AnsysTutorial/IT/Density/Density.html
Author: Berke Kadioglu