TA1: Heat Transfer from a Cooling Spine

1. PROBLEM DESCRIPTION

A rod with have a square cross-section is fixed from the Wall. The cross-sectional area and length of the rod are given. The convection coefficient and ambient temperature of the air around the rod are known. The cooling of the rod with the convection boundary condition of the air will be examined. We will calculate Heat Flux and the tip of temperature when it comes to steady-state, a rod that wall temperature is known and the other side is insulated.

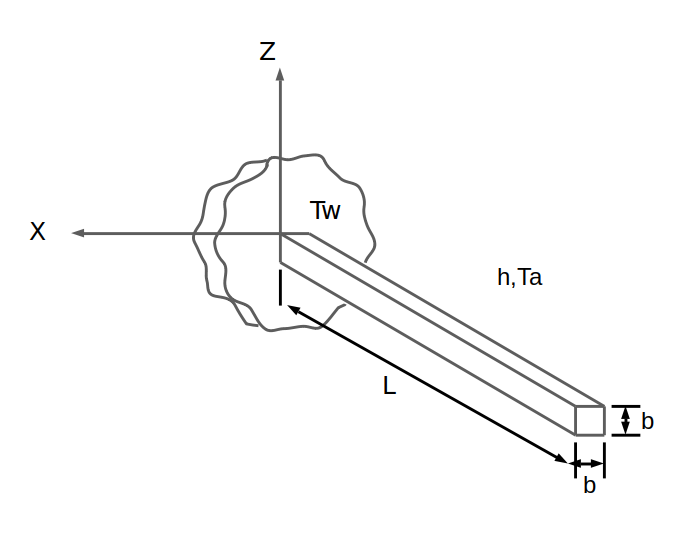
../_images/HeatTransferFromCoolingSpine1.png
Properties and BC Value

Material Properties

Geometric Properties

Loading

k = 25 Btu/hr-ft-°F

L = 8 in = (2/3) ft

Ta = 0°F

h = 1 Btu/hr-ft2-°F

b = 1 in = (1/12) ft

Tw = 100°F

2. MODEL SETUP AND SOLUTION

The following sections describe the setup and solution steps for this tutorial:

2.1. Preparation

2.2. General Settings

2.3. Geometry/Mesh

2.4. Material

2.5. Boundary Conditions

2.6. Solution

2.7. Processing

2.8. Post-Processing

2.1. Preparation

To run this tutorial;

  1. You must sign up and log in. —->>>>> TwinAPI

  2. After login, Click Personel Projects>>New Project button on the screen and then we will create a project page by giving the project name.

(Let’s name of Analysis “TempDistFin1”)

  1. You can see the project page on your Personel Project Part.

  2. Our Screen is a blank python page without any script. We will be doing a tutorial by using Simularge’s Library.

../_images/HeatTransferFromCoolingSpine4.png ../_images/HeatTransferFromCoolingSpine5.png ../_images/HeatTransferFromCoolingSpine6.png

  1. We import our libraries from the Simularge Libraries to our empty Python page that we almost will use in each tutorial.

1from TwinAPI.SimulationTools import Solver
2from TwinAPI.SimulationTools import Mesher

Material Properties is one of the most significant factor that affect to result. Therefore,we should define it easily to the problem. I will explain below how to use and write Material Library elaborately. Furtherless, The Libraries that has to imported to problem is given below.

1from TwinAPI.MaterialLibrary import MaterialManager
2from TwinAPI.MaterialLibrary.Units import units

2.2. General Settings

After the necessary libraries are imported into the analysis, analysis are defined.

  1. Defined name of Analysis as “TempDistFin1”

1TempDistFin1= Solver.Analysis(Verbose=True)

  1. Calculix is used on solid mechanics problems in TwinAPI. Hence, we are defining Calculix to run this analysis.

1TempDistFin1.SetSolver("corefem")

Analysis is defined successfully into TwinAPI System.

../_images/HeatTransferFromCoolingSpine7.png

2.3. Geometry/Mesh

There is two different options to define geometry on TwinAPI System. Create own geometry on TwinAPI by using Mesher Library that belong to Simularge’s libraries or You can import own CAD Geometry.

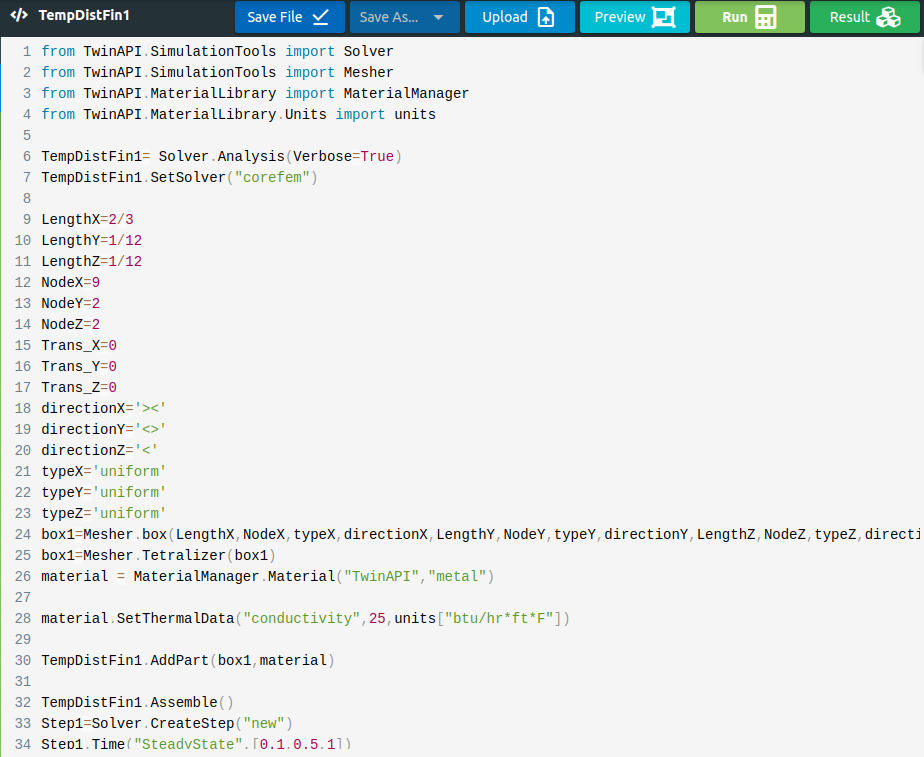
 1    LengthX=2/3
 2    LengthY=1/12
 3    LengthZ=1/12
 4    NodeX=9
 5    NodeY=2
 6    NodeZ=2
 7    Trans_X=0
 8    Trans_Y=0
 9    Trans_Z=0
10    directionX='>'
11    directionY='<>'
12    directionZ='<'
13    typeX='uniform'
14    typeY='uniform'
15    typeZ='uniform'
16    box1=Mesher.box(LengthX,NodeX,typeX,directionX,LengthY,NodeY,typeY,directionY,LengthZ,NodeZ,typeZ,directionZ,Trans_X, Trans_Y, Trans_Z)

With the script given above, you can create your box geometry and mesh.

LengthX= Length of X Direction

NodeX= Node Number of X Direction

Trans_X= Translation of X Direction

directionX= Aspect

typeX= Mesh type of X direction.

All of given above is valid for Y and Z Direction.

We create a box geometry that name is “box1” from given inputs.

Note

We told you that you can also create this geometry import 3D CAD file apart from using MESHER. Code should be written like this;

1 Box1=Mesher.MeshFromCad('Box.step',20000,1,1e4,SurfaceExtract=True)

If we are not sure how created geometry and want to see geometry before starting analysis;

Click Preview Button

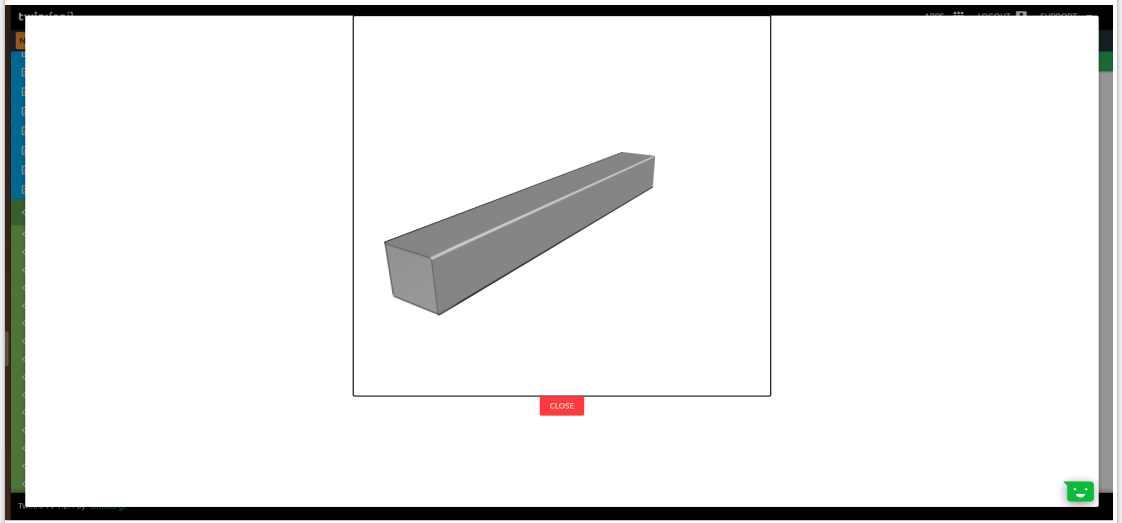
../_images/HeatTransferFromCoolingSpine8.png ../_images/HeatTransferFromCoolingSpine9.png

2.4. Material

Before we started,There are lots of parameters to impact to result of problem. We are going to explain which parameters are requirement for problem first. Later, We would give an parameters instances which can be used.

If your material is isotropic thats means all properties is equal with different direction. However Anisotropic Material Properties is not the same value with different direction. Only Thermal Conductivitiy of material will impact amount of heat transfer in this problem.

We call the Material class in the Material Manager library and name the material “TwinAPI”. At the same time, We give the information that the material behaves as a metal by typing “metal”.

Although not necessary, We have written the conductivity properties in all directions below. But it would be enough if we just write it in the X direction because my material is isotropic.

1 material = MaterialManager.Material("TwinAPI","metal")
2
3
4 material.SetThermalData("conductivity",25,units["btu/hr*ft*F"])

We will make an example to understand better what can be used parameters in Material Library.

1 material.SetThermalData("specificHeat",7,units["j/kgk"])
2
3 material.SetThermalData("expansionCoefficient",10,units["1/k"])
4
5 material.SetGeneralData("density",5,units["kg/m3"])

After defining the material into our system, we should combine geometry define above and material using Addpart method.

1TempDistFin1.AddPart(box1,material)
2
3TempDistFin1.Assemble()

2.5. Boundary Conditions

After adding material and geometry to the analysis, we are ready to set the boundary conditions.

  1. First of all, we need to call a method to create a step. Step1’s name can be change.

1Step1=Solver.CreateStep("new")

  1. We need to choose whether this step is computed depending on time or not.Explained problem is Steady-State. Therefore,below code should be written.

1Step1.Time("SteadyState",[0,0.5,0.1])

If the Problem was Transient,type of problem and time of analysis should be written in a similar manner with below code.

1Step1.Time("Transient",[0,10,0.1])

  1. The type of boundary conditions required for the problem are temperature and convection. Also, since the right side of the box is insulated, it is assumed that there is no heat transfer there. The ambient temperature and h (Heat Transfer Coefficient) value required for the problem can be defined before the boundary conditions are stated.

 1AmbientTemperature = 0
 2
 3h=1
 4
 5Step1.AddBC("Temperature",[box1.left],[100],"F")
 6
 7Step1.AddBC("Convection",[box1.top],[(AmbientTemperature,h)],"")
 8
 9Step1.AddBC("Convection",[box1.bottom],[(AmbientTemperature,h)],"")
10
11Step1.AddBC("Convection",[box1.front],[(AmbientTemperature,h)],"")
12
13Step1.AddBC("Convection",[box1.back],[(AmbientTemperature,h)],"")
14
15Step1.AddBC("Heat Flux",[box1.right],[0],"")

2.6. Solution

After defining our boundary conditions, we need to combine our defined domain and the steps containing boundary conditions.To complete this task;

1TempDistFin1.Build([Step1])

Now,Problem is ready to be solved.

1TempDistFin1.Solve()

Before going to be PostProcess Stage, we can review what we have done.

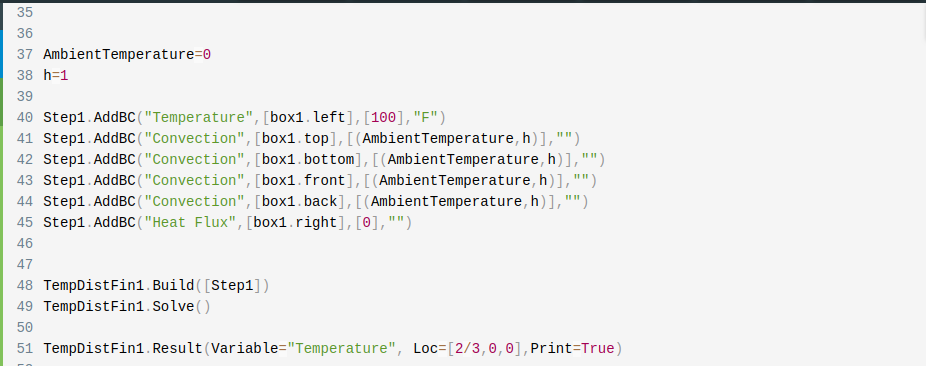
../_images/HeatTransferFromCoolingSpine10.png ../_images/HeatTransferFromCoolingSpine11.png

2.7. Processing

  1. Click Run Button and gears rotate on right side while problem is being solved.

../_images/HeatTransferFromCoolingSpine12.png

2.8. Post-Processing

  1. After Problem solved;

We can see result;

Click Result Button

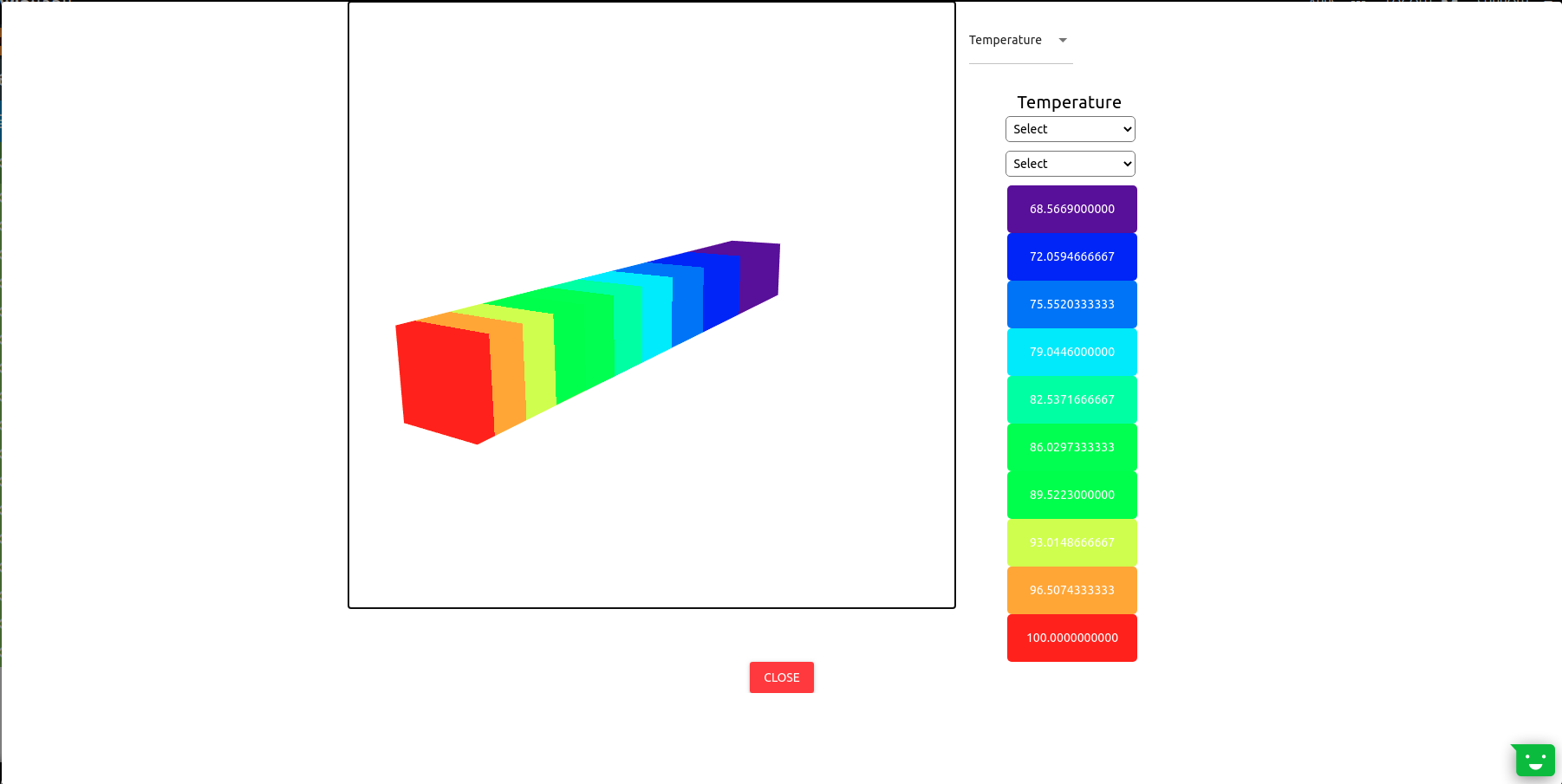
../_images/TemperatureDistributionShortSolidCylinder51.png ../_images/HeatTransferFromCoolingSpine13.png

  1. If we want to see detailed result about problem;

../_images/HeatTransferFromCoolingSpine14.png

Output Tab shows us the results that we desire to see. If Print=False,We couldn’t see anything in the Output section.

1TempDistFin1.Result(Variable="Temperature", Loc=[2/3,0,0],Print=True)
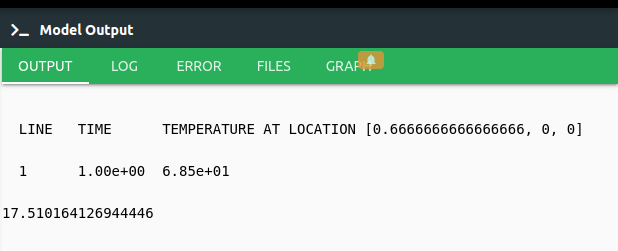
../_images/HeatTransferFromCoolingSpine15.png

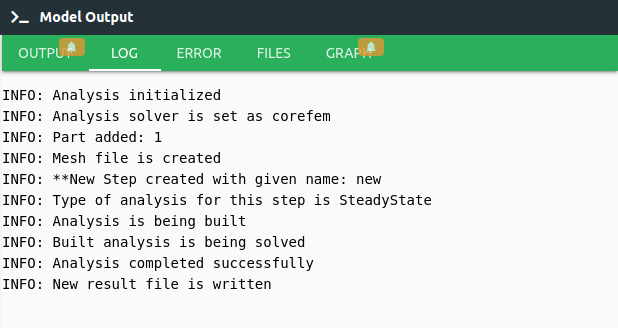
Log tab tells us respectively what happened in analysis.

Error tab shows us if there is an error in script, It tells us what the error is and where it is.

Files tab can upload the files to be imported from the Upload command and check them from Files.

Graph tab shows us analysis result can be viewed graphically. (It will be shown in other examples.)

In the problem example, result information is also given for heat flux. In the post-processing stage, heat flux information cannot be seen at the moment. If you are wondering how we found the Heat Flux given in the Output, it will be enough to write the following after the “TempDistFin1.Solve()” code.

 1    TempList=[]
 2    import numpy as np
 3    for x in np.linspace(0,LengthX,NodeX):
 4
 5
 6         res=TempDistFin1.Result(Variable="Temperature", Loc=[x,0,0],Print=False)
 7         temp=res[0,1]
 8         TempList.append(temp)
 9
10    SurfaceList=[]
11
12    for Surface in range(NodeX-1):
13        TempList[Surface]
14        TempList[Surface+1]
15        SurfaceTemp=(TempList[Surface+1]+TempList[Surface])/2
16
17        SurfaceList.append(SurfaceTemp)
18
19    Area=LengthY**2
20
21    EnergyPerSurface=0
22
23
24    for SurfaceTemp in SurfaceList:
25        DeltaT=SurfaceTemp-AmbientTemperature
26        HeatFl=h*DeltaT
27        EnergyPerElement=HeatFl*Area
28        EnergyPerSurface+=EnergyPerElement
29
30
31    TotalEnergy=EnergyPerSurface*4
32
33    print("Total Energy:",TotalEnergy,"BTU/hr")

3. SUMMARY

In this tutorial, we learned how to set up and solve a problem involving temperature and natural convection on a rod on TwinAPI. We also learned how to perform postprocessing in an engineering manner.

With table given below shows that comparasion of Ansys Mechanical Result and TwinAPI result.

Comparasion

SOLID MODEL

Target

ANSYS

SIMULARGE-TwinAPI

Ratio: SIMULARGE/Target

Ratio: SIMULARGE/ANSYS

T_length, °F

68.594

68.618

68.566

1.00

1.00

q, Btu/hr

17.504

17.528

17.520

1.00

1.00

4. SOURCE CODE

 1from TwinAPI.SimulationTools import Solver
 2from TwinAPI.SimulationTools import Mesher
 3from TwinAPI.MaterialLibrary import MaterialManager
 4from TwinAPI.MaterialLibrary.Units import units
 5
 6TempDistFin1= Solver.Analysis(Verbose=True)
 7TempDistFin1.SetSolver("corefem")
 8
 9LengthX=2/3
10LengthY=1/12
11LengthZ=1/12
12NodeX=9
13NodeY=2
14NodeZ=2
15Trans_X=0
16Trans_Y=0
17Trans_Z=0
18directionX='><'
19directionY='<>'
20directionZ='<'
21typeX='uniform'
22typeY='uniform'
23typeZ='uniform'
24box1=Mesher.box(LengthX,NodeX,typeX,directionX,LengthY,NodeY,typeY,directionY,LengthZ,NodeZ,typeZ,directionZ, Trans_X, Trans_Y, Trans_Z)
25box1=Mesher.Tetralizer(box1)
26material = MaterialManager.Material("TwinAPI","metal")
27
28material.SetThermalData("conductivityX",25,units["btu/hrftf"])
29
30TempDistFin1.AddPart(box1,material)
31
32TempDistFin1.Assemble()
33Step1=Solver.CreateStep("new")
34Step1.Time("SteadyState",[0,0.5,0.1])
35
36
37AmbientTemperature=0
38h=1
39
40Step1.AddBC("Temperature",[box1.left],[100],"F")
41Step1.AddBC("Convection",[box1.top],[(AmbientTemperature,h)],"")
42Step1.AddBC("Convection",[box1.bottom],[(AmbientTemperature,h)],"")
43Step1.AddBC("Convection",[box1.front],[(AmbientTemperature,h)],"")
44Step1.AddBC("Convection",[box1.back],[(AmbientTemperature,h)],"")
45Step1.AddBC("Heat Flux",[box1.right],[0],"")
46
47
48TempDistFin1.Build([Step1])
49TempDistFin1.Solve()
50
51TempDistFin1.Result(Variable="Temperature", Loc=[2/3,0,0],Print=True)

Keywords: Heat Transfer, Cooling,Convection, Temperature, Heat Transfer Coefficient

Problem Reference: F. Kreith, Principles of Heat Transfer, 2nd Printing, International Textbook Co., Scranton, PA, 1959, pg. 48, eq. 2-44, 45.